Participatory random numbers in Ethereum
· Jim McDonald · 8 minutes read · 1611 words ·Random numbers are useful for many purposes in computing, from deciding the order when shuffling tracks in a playlist to picking lottery numbers. A common case for use of random numbers is in gambling: two or more players (generically known as participants) bet on the outcome of a game. In this situation it is vitally important that the outcome of the game is based on fair random numbers. Importantly, if one participant knows the numbers in advance then the game can no longer be considered fair as they can raise or lower their bet according to what they know will be the outcome of each round of the game.
It is possible to generate fair random numbers with two or more participants acting together. This is called participatory random number generation, and results in numbers that are unknowable by any party beforehand. It is also trustless, in that none of the participants can affect the numbers without being caught. Participatory random numbers form the basis for games that can be carried out online with Ethereum acting as the validator for the random numbers.
This article explains how participatory random numbers work by combining two separate features: repeated hashing and participatory contribution.
Number generation through repeated hashing
Repeated hashing is a well-known method of generating a stream of values. A good hash function takes an input and generates an output, with the following important features:
- running the hash function is relatively inexpensive (in terms of CPU time)
- all outputs of the hash function are equiprobable
- it is not feasible to go from the output of the hash function back to the input
Ethereum’s main hash function is keccak256() so this will be used for the rest of this article and referred to simply as \(H()\). \(H()\) outputs a 32-byte value, and for brevity all 32-byte values will be shown only by their first and last two bytes e.g. \(0x1234…5678\)
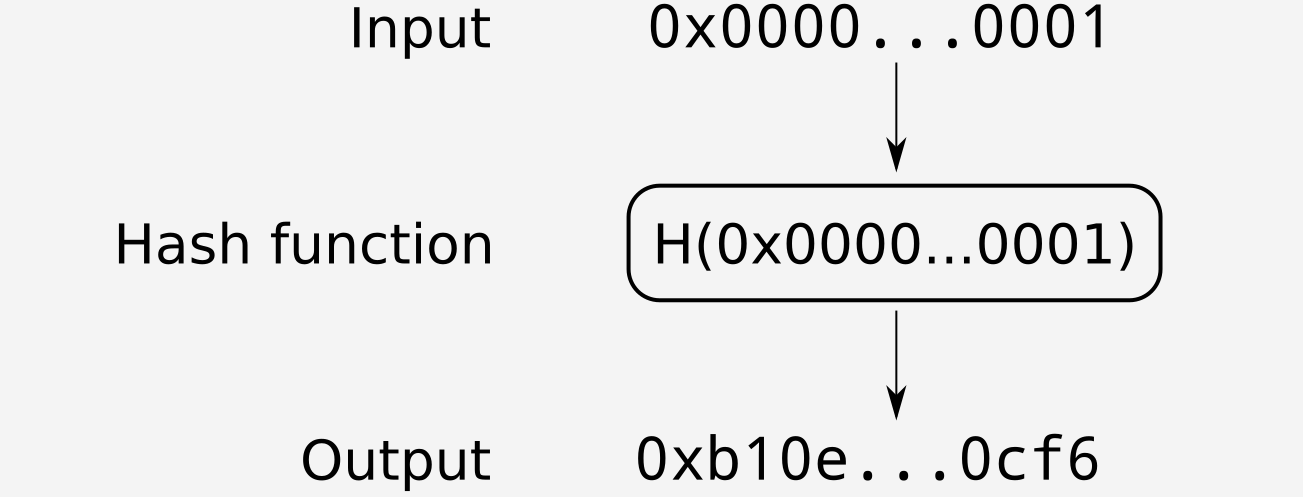
Figure 1: Hashing a value
Repeated hashing is the act of running the hash function multiple times, using the output of one run of the hash function as the input of the next run. For the rest of this article repeated hashing will be referred to as \(H_{n}()\) , with n being the number of times that the hash function is run.
Continuing the example started above, the repeated hash table for \(0x0000…0001\) is as follows:
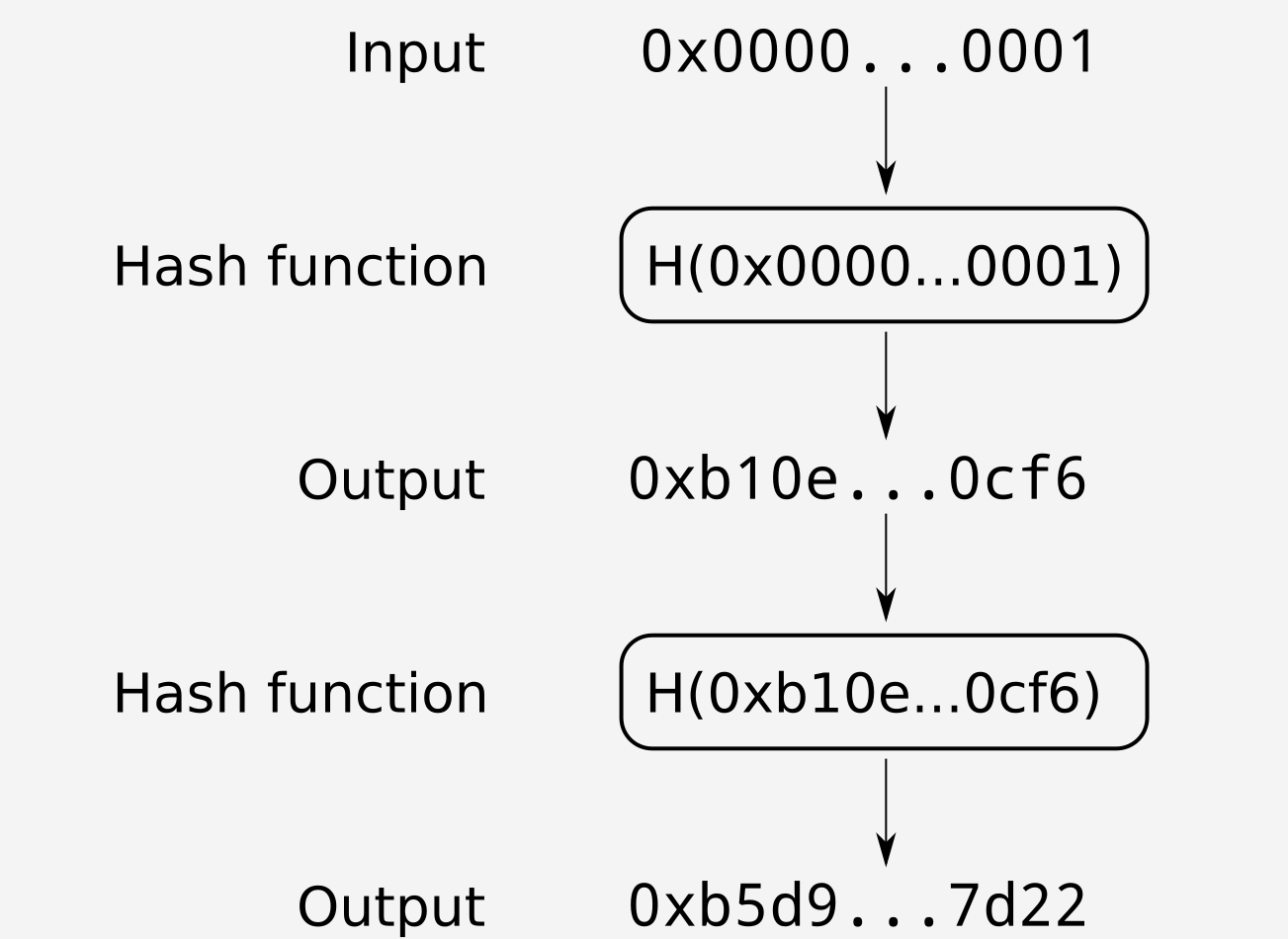
Figure 2: Hash table starting at $0x0000…0001$
A slightly different input produces a completely different output. Repeating the above table starting with \(0x0000…0002\) as the first input provides the following table:
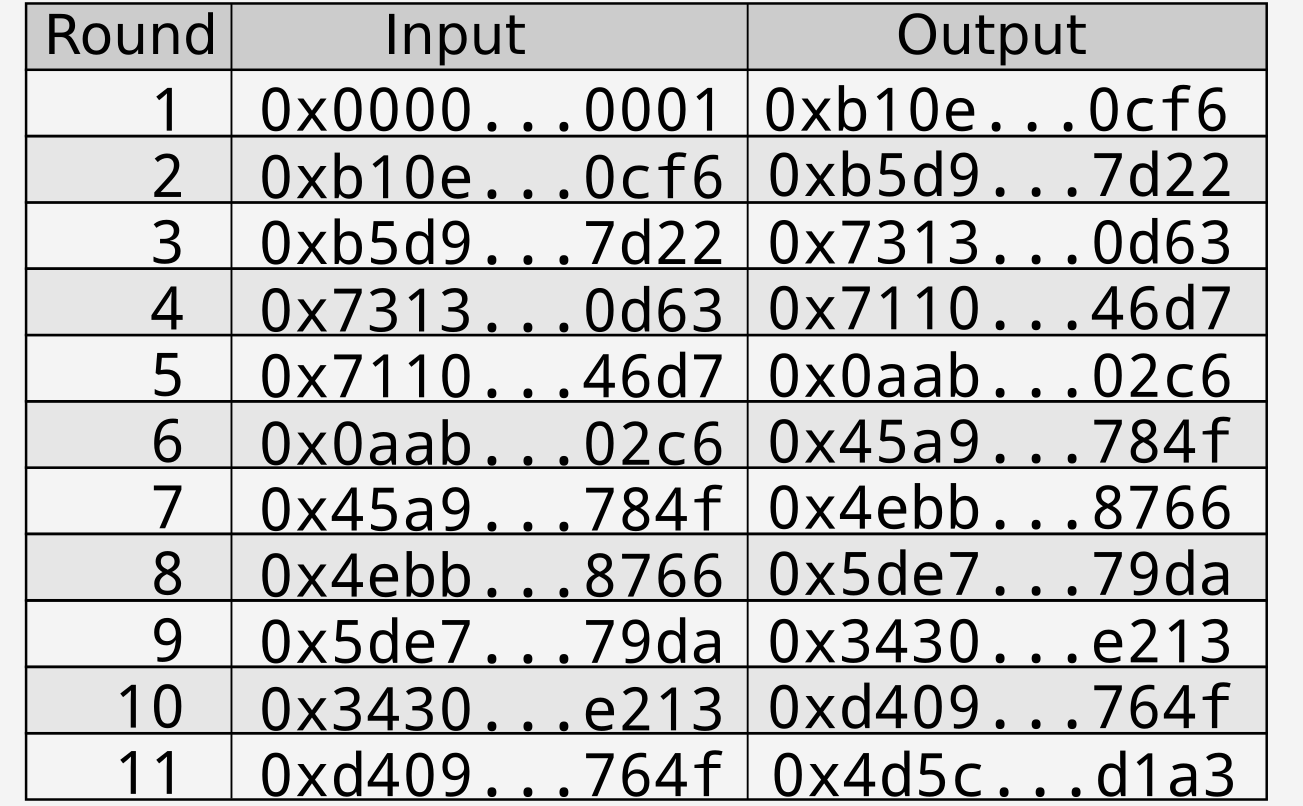
Figure 3: Hash table starting at $0x0000…0002$
It should be clear from the definition of repeated hashing that \(H_{n}() \equiv H(H_{n-1}())\) for any \(n \gt 0\).
Recall from earlier that the features of a hash function include the ability to calculate a later output quickly and easily from an earlier output and the inability to do the opposite. As such, a participant starting with \(0x0000…0001\) could store \(H_{11}(0x0000…0001)\) in a smart contract and at a later point in time publish \(H_{10}(0x0000…0001)\) . Outside parties can verify that the published value is correct by hashing the published value i.e. \(H(H_{10}(0x0000…0001))\) and comparing it to the value stored in the smart contract.
Hence once each participant announces their final output (in the above examples \(0x4d5c…d1a3\) for the first participant and \(0x4c97…842f\) for the second participant) they are locked in to their values for the earlier rounds without needing to announce the information in advance. This gives each participant trust that the other participants have not tampered with their numbers.
Participatory contribution
The previous section explained how each participant can provide a number that cannot be guessed in advance by other participants but is easily verifiable as not having been tampered with. Participatory contribution is a mechanism to build a single value from the contributions of multiple participants, with each participant’s contribution altering the final value in such a way that no one participant has any advantage over the others in knowing how their contribution will shape the final value.
Taking a simple example with two participants: each participant contributes a 32-byte value and these are combined using the XOR function to provide a single agreed-upon value. This is shown below:
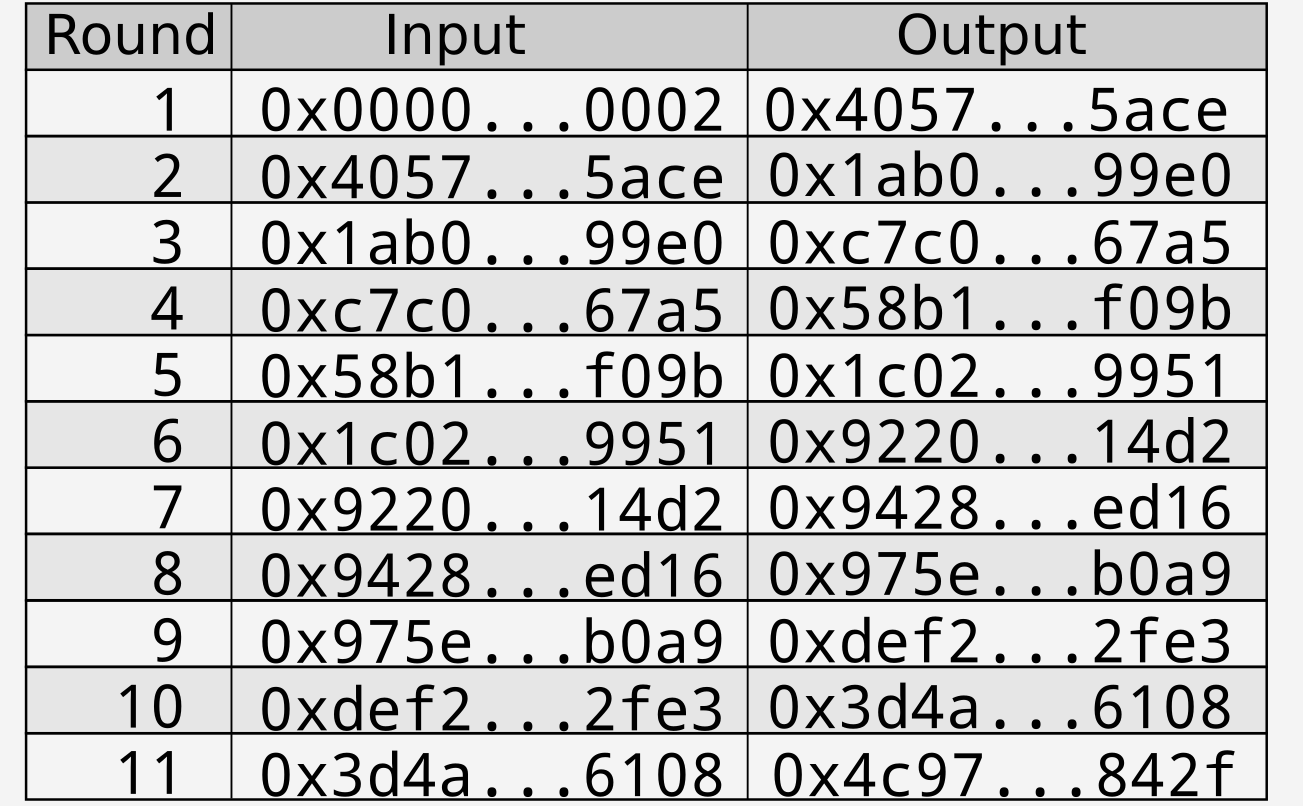
Figure 4: XORing two contributions to obtain a resultant value
Neither participant can choose their contribution to alter the likelihood of the output value without knowing the contribution of the other party.
Importantly, as long as at least one of the participants is trustworthy the output will be trustworthy. Hence any participant can trust the result of the XOR function as long as they themselves have not colluded with the other parties.
Random number generation
Repeated hashing and participatory contribution can be combined to provide random numbers in an Ethereum smart contract. Continuing the example of two participants the process goes as follows:
- one participant sets up the game with the maximum number of rounds; in this example 10
- each participant chooses their initial value (known as the seed), generates \(H_{11}()\) of their seed, and publishes it (known as the source)
- before round 1 starts both parties place bets on the outcome of the round
- at round 1 both participants present the value of \(H_{10}()\) of their seeds to each other
- the two values are combined to produce a final random value for round 1, which is used to determine the outcome of the round
- for further rounds the previous two steps are repeated (so for round 2 each participant presents \(H_{9}()\), for round 3 each participant presents \(H_{8}()\), etc.)
Prior to the first round both parties only know their own value of \(H_{10}()\), so they bet without having any knowledge of the outcome. When each participant reveals their own \(H_{10}()\) the other participant can confirm that it is valid by ensuring that \(H(H_{10}())\) is the same as the participant’s published source (as \(H(H_{10}())==H_{11}())\). Both participants agree on the random number generated from combining their \(H_{10}()\) values and hence the outcome is considered fair.
On-chain and off-chain work
Participatory random number generation carries out most of its work off-chain. This is important, as Ethereum transaction times are variable and would make many online games either too slow or too expensive to undertake. All that needs to happen on-chain is for the instance to be created and each participant to store the final output of their hashing, for example in the case of a 10-round game each participant would store \(H_{11}()\) of their seed. Generation of the random number for each round can be carried out off-chain, as can validation of each participant’s value.
Real-world example
What follows is a complete example of using participatory random numbers with two parties to generate trustless and fair random numbers. The full contract⧉ is available for reference.
The first step is to deploy the contract. Once it has been deployed an instance is created by either participant sending a newInstance() transaction to the contract with an instance ID of 1 and number of rounds 10:
newInstance(1, 10)The first participant selects \(0x0000…0001\) as their seed and the second participant selects \(0x0000…0002\) as their seed (note that these are examples; each participant in reality should choose a random value as their seed). Both parties hash their seed 11 times (one more than the number of rounds) to obtain the source and submit it to the contract with a setSource() transaction, so the first participant submits
setSource(1, 0x4d5c…d1a3)and the second participant submits
setSource(1, 0x4c97…842f)At this point the instance is ready. The two participants each agree upon the round number (as this is the first round the number is 1) and calculate their contribution value using an off-chain call to generateValueFromSeed(), so the first participant calls
generateValueFromSeed(1, 0x0000…0001, 1)to receive \(0xd409…764f\) and the second participant calls
generateValueFromSeed(1, 0x0000…0002, 1)to receive \(0x3d4a…6108\).
They share their value with the other participant and each participant independently calls generateRandomValue() which confirms that all participants’ values are correct and calculates the resultant random value, so
generateRandomValue(1, [a1, a2], 0, [0xd409…764f, 0x3d4a…6108])to receive \(0xe943…1747\). Note that in the above call a1 is the address of the first participant and a2 is the address of the second participant.
Both participants can now use the generated random value \(0xe943…1747\) knowing that it is suitably random and that the other participant could neither influence nor predict it.
Notes on use
Once generated the random number can be used for any purpose by using an agreed-upon rule to decide how to use it. To take a simple example: if two participants use the generated number to select a “winner” they can do so by agreeing beforehand that the first participant takes the first two bytes of the number and the second participant takes the last two bytes of the number, and whomever has the higher result is considered the winner. Using the number generated in the last section the first participant would have \(0xe943\) as their number and the second participant \(0x1747\) as their number so the first participant wins this round.
The round number in an instance should never be re-used, and should always increase. For example, if a game is played for round 5 then the next game must have a higher round number (6 or more).
Although the examples in this article use two participants and ten rounds, the contract works for any number of participants and rounds. It can easily be extended to tens of players and thousands of rounds without significant CPU impact, however if the calculations are ever made on-chain, for example as part of a validation transaction, then it is important to understand the impact on gas of higher rounds and more participants.